6-DOF Wire-Driven
Haptic Interface

SPIDAR-GⅡ is a wire-driven 6-DOF high performance haptic display device. The device is composed of wires, pulleys and DC motors.
These elements have a signficant reduction of the inertia because of their lightwaight proprieties, compared to other architectures of haptic
devices. Built-in HC (Haptic Controller) with encoder counters, motor drivers and USB 2.0 interface enables prominent calculations at hardware
level. As a result, SPIDAR-GⅡ with HC realizes high performance with stable haptic sensations.

SPIDAR, which stands for ‘SPace Interface Device for Artificial Reality’, is a series of string-based haptic interface device. Since its first version developed by Dr. Makoto SATO in 1989, SPIDAR has emerged as a distinguished haptic interface capable of displaying various aspects of force feedback. The usage of string-based technology to track user’s hands’ or fingers’ position as well as display force feedback leaves the system with less weight, better scalability and better flexibility. Still, the quality of SPIDAR’s haptic feedback continues improving through time to reach the current standard, and in line with other major haptic systems, of accurate measurements and smooth force display.


1) Calculation of pointer’s current position and orientation vector,

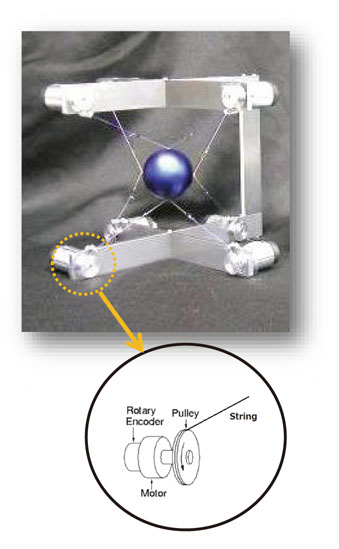
Among several versions of SPIDAR, SPIDAR-G is a grip-type, tension- based 6-DOF haptic interface
with 8 strings and 8 driving motors.
As shown in the figure beside, for each string, one end is connected to the grip; the other end is
attached to the pulley settled around the axis of a DC motor.
For each driving motor, a rotary encoder is attached to measure the string’s length. With the current
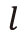
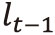
encoder value vector and the encoder value vector at the last clock cycle, , the variation of string’s
length can be calculated by formula (1).

                                 (1)

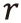
Then, while stands for the pointer’s current position and orientation vector, difference between
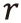
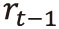
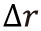
and , the pointer’s position and orientation vector at the last clock cycle, can be approximately
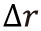
calculated by solving formula (2). Here, stands for the difference.

                                       (2)

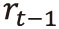
In formula (2), stands for the Jacobian matrix which depends on and .
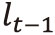
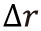
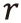
Once is calculated, the present positionand orientation vector is updated as formula (3).

                           (3)

2) Distribution Calculation for actuator’s torque

To reproduce forces with given magnitude and direction, distribution calculation based on quadratic
programming is performed to assign proper output torque to every single driving motor.
Resultant force of strings' tension acting upon the grip is supposed to be the same as the expected force.
Force display can be used to reproduce virtual object’s weight and material, state of motion,
as well as interaction forces between multiple virtual objects.

Force Feedback	6DOF x, y, z, Tx, Ty, Tz
Position Setting	6DOF x, y, z, Roll, Pitch, Yaw
Workspace	150(W) x 150(H) x 190(D) mm
Maximum Force	2.0 N (Translation), 0.001 rad (Angle)
Motor	DC Motor x 8
Encoder	512 pulse / turn
Frequency	1 kHz
Interface	USB 2.0
OS	Windows 7 / 10